Bollinger Bands - 布林通道/保力加通道¶

由約翰·保力加 (John Bollinger) 所發展的保力加通道 (Bollinger Bands) 是波動通道，置於移動平均線的上下方。波動性(volatility)基於標準差，標準差會隨著波動率的上升和下降而變化。通道會隨著波動率的上升自動擴大，並隨著波動率的下降而收窄。其動態特性使其能夠在使用標準設定的不同證券上進行應用。

如何有效使用保力加通道呢？它可以用於識別雙頂 (M-Tops) 和雙底 (W-Bottoms)，或確定趨勢的強弱。

計算方法¶

    上均線= 20-日均線 + 2倍標準差
    均線  = 20-日均線
    下均線= 20-日均線 - 2倍標準差

應用例子 - 雙底¶

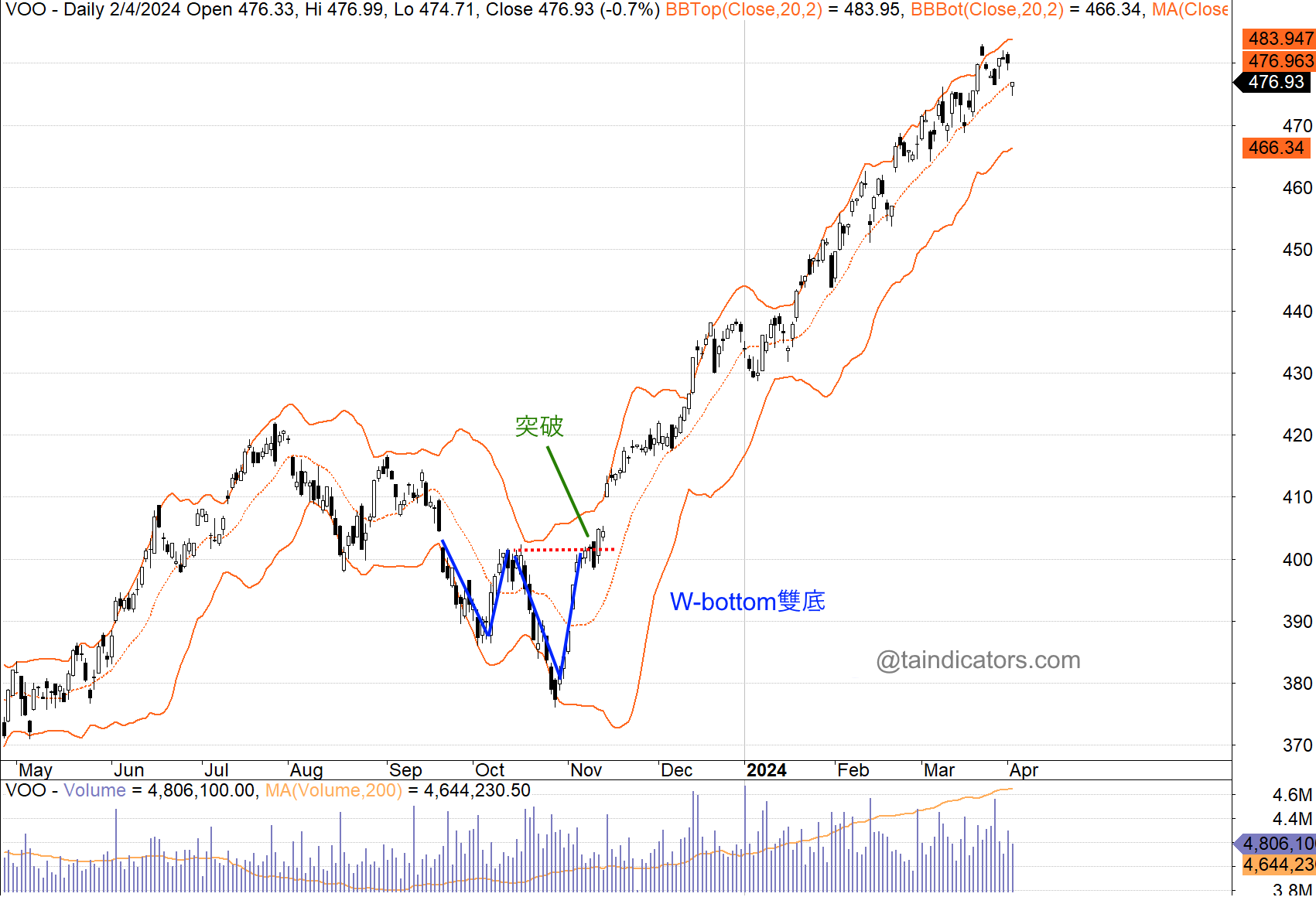
雙底在下降趋势中形成，包含兩個反彈低點。保力加特别关注第二個低點比第一個低點更低，但仍高於下通道的雙底形態。使用保力加通道确认雙底有四个步骤。

首先，形成一個反彈低點。這個低點通常（但并非总是）會低於下通道。
其次，價格會反彈靠近中線。
第三，該證券出現新的價格低點。這個低點高於下通道。在測試中能夠守住下通道，表明最近的下跌力度較弱。
第四，該形態通過強勁反彈脫離第二個低點以及突破阻力位得到確認。

下圖是 Thomson Reuters (TRI.US) 2023 年 9 月至 11 月的W形雙底形態。形成第二底點時有二天底於下通道,但很快返回通道內並突破阻力。

Bollinger Bands

應用例子 - 雙頂¶

保力加建議在股票創出新高時尋找背馳訊號來識別雙頂形態。背馳訊號包含以下三個步驟。

首先，該證券的價格會創造出高於上通道的回升高點。
其次，價格回落靠近中線。
第三，價格雖然升破前高，但未能觸及上通道。這是一個警示信號。

第二個迴升高點無法觸及上通道顯示動能減弱，這可能預示著趨勢即將反轉。最終確認來自支撐位跌破或看跌指標訊號。

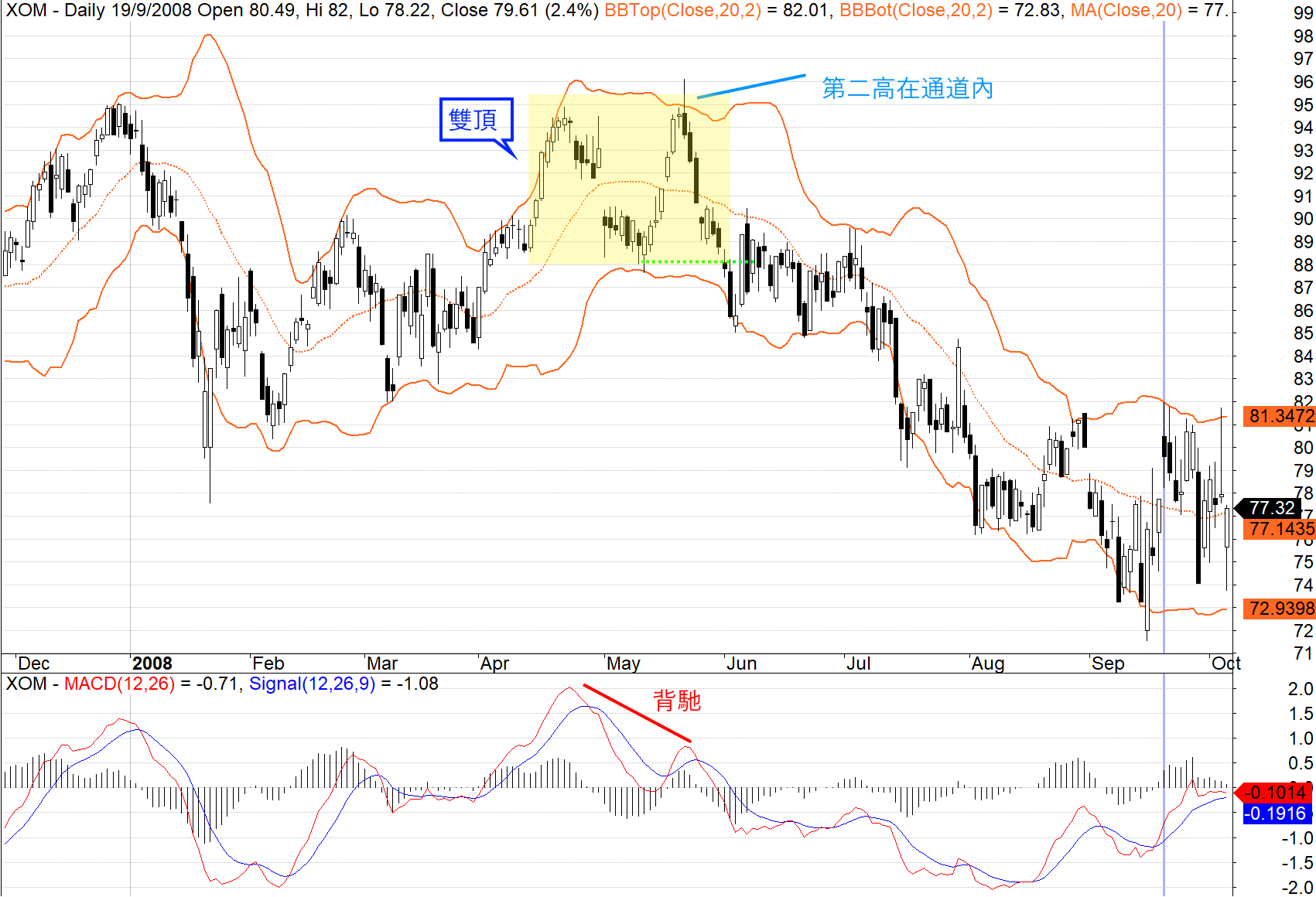
Bollinger Bands

上圖顯示了埃克森美孚(XOM.US) 在 2008 年 4 月至 5 月出現的雙頂。該股 4 月突破上通道，然後 5 月回落，再次上漲突破 90 美元。儘管該股盤中一度突破上通道，但收盤價並未突破上通道。突破支撐位兩週後，M 頂確認。此外，MACD 指標形成看跌背馳並下穿訊號線，進一步確認頂部成立。

沿著保力加通道行走¶

價格在保力加通道上方或下方的移動本身並不是買進/賣出訊號。正如保力加所說，觸及或超過通道的走勢不是訊號，而是「標籤」。表面上，價格漲到上通道顯示強勢，而急跌至下通道則顯示弱勢。動量振盪指標(Momentum oscillators)的工作原理大致相同。超買不一定是看漲。達到超買水準需要力量，超買狀況可能會在強勁的上升趨勢中延續。同樣，在強勁的上升趨勢中，價格可以走在區間內多次觸及上通道。想一想。上通道比 20 週期簡單移動平均高 2 個標準差。價格走勢需要相當強勁才能超過這個上通道。保力加通道確認 W 底後觸及上通道將標誌著上升趨勢的開始。正如強勁的上升趨勢會產生大量的上軌線標籤一樣，價格在上升趨勢期間永遠不會達到下軌線是很常見的。 20 日移動平均線有時會起到支撐作用。事實上，跌破 20 日均線有時會在下一個上升之前提供買入機會。

不要單獨使用保力加通道¶

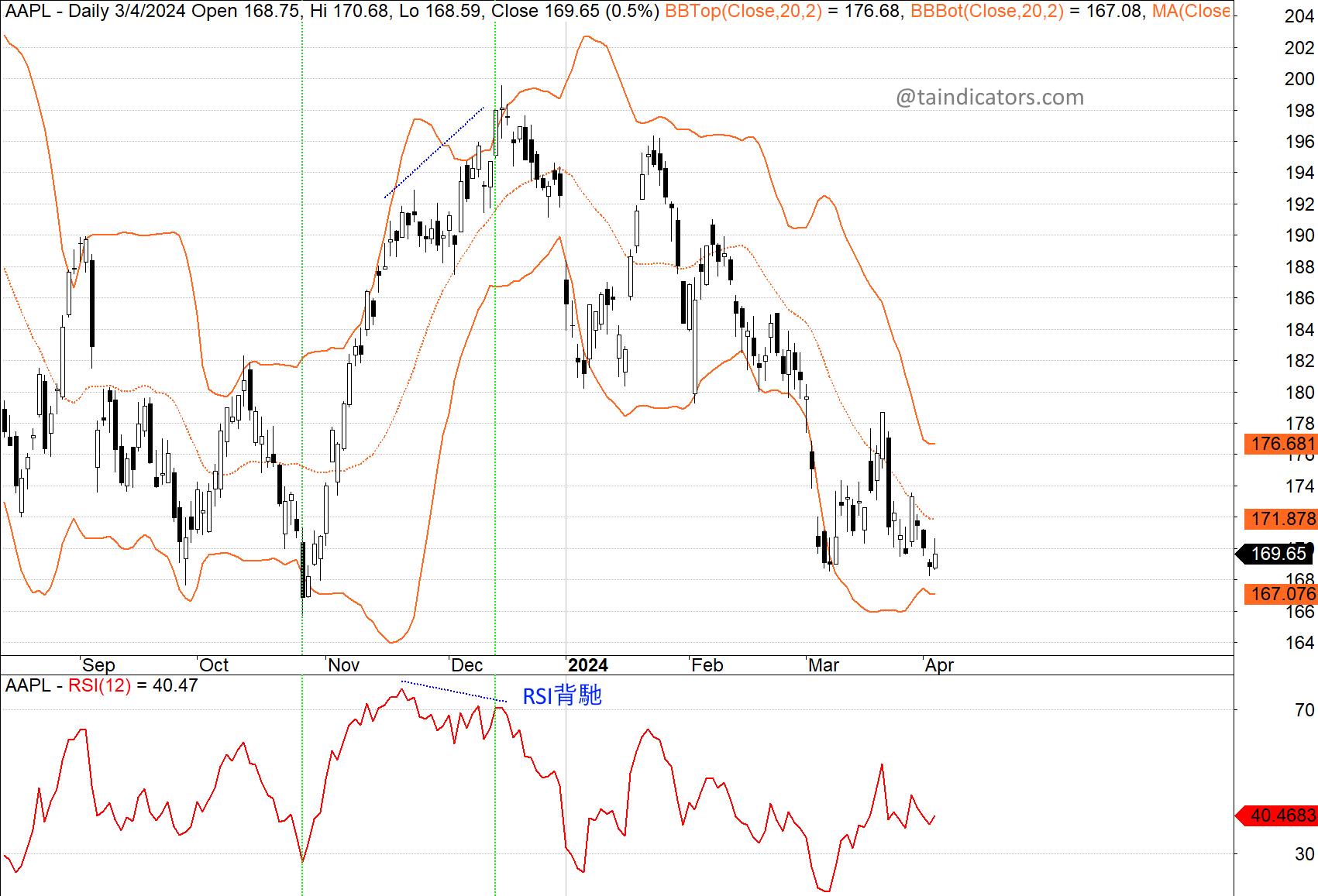
需要記住的重要一點是，保力加通道不會單獨產生買賣訊號。保力加通道應該與另一個指標一起使用。例如，RSI 是一個不錯的選擇。當價格觸及其中一條通道時，可能表明兩件事之一: 它可能顯示趨勢的延續；因此，保力加通道本身並不能提供技術人員需要了解的所有資訊。然後，RSI可提供幫助。一般來說，當價格觸及保力加通道上軌且RSI低於70時，我們有跡象表明趨勢將持續。相反，當價格觸及保力加下軌且 RSI 高於 30 時，我們有跡象表明趨勢應該持續。如果我們遇到價格觸及布林通道上軌且 RSI 高於 70（可能接近 80）的情況，我們就有跡象表明趨勢可能會反轉並向下移動。另一方面，如果價格觸及保力加通道下軌且 RSI 低於 30（可能接近 20），我們就有跡象表明趨勢可能會反轉並向上移動。如果您將 RSI 與保力加通道結合使用，不要同時使用 MACD,它們RSI與MACD都依賴相同的輸入資料。您可以考慮使用OBV或資金流。 RSI、OBV和資金流量依賴不同的輸入資料。

Bollinger Bandsn and RSI